Численное решение дифференциальных уравнений

Решение с начальными условиями

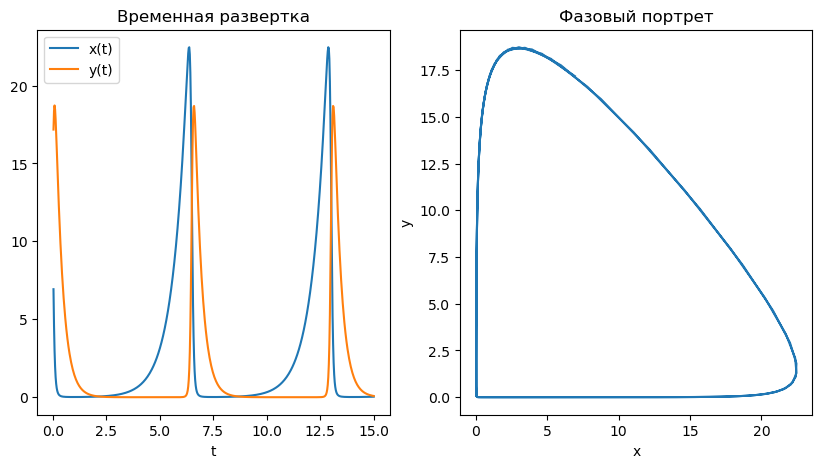
Итеративное решение на примере модели Лотка-Вольтерра

from scipy.integrate import ode
import matplotlib.pyplot as plt
import numpy as np

# Система уравнений
def f(t, u):
    x, y = u
    dx = 1.5*x - x*y
    dy = -3*y + x*y
    return [dx, dy]

# Создание объекта - интегратора системы
r = ode(f).set_integrator('vode', method='adams',
                          order=10, atol=1e-6,
                          with_jacobian=False)

# Задание начальных условий
u0 = [10, 15]
r.set_initial_value(u0, 0)

# Время и шаг по времени
T = 15
dt = T/600.

# Выходные переменные
u = [];  t = []

# Итеративное вычисление
while r.successful() and r.t <= T:
    r.integrate(r.t + dt)
    u.append(r.y);  t.append(r.t)

# Рисование

fig = plt.figure(figsize=(10,5))
ax1 = fig.add_subplot(1,2,1)
ax1.plot(t, np.array(u).T[0], label='x(t)')
ax1.plot(t, np.array(u).T[1], label='y(t)')
ax1.legend()
ax1.set_title('Временная развертка')
ax1.set_xlabel('t')

ax2 = fig.add_subplot(1,2,2)
ax2.plot(np.array(u).T[0], np.array(u).T[1])
ax2.set_title('Фазовый портрет')
ax2.set_xlabel('x')
ax2.set_ylabel('y');

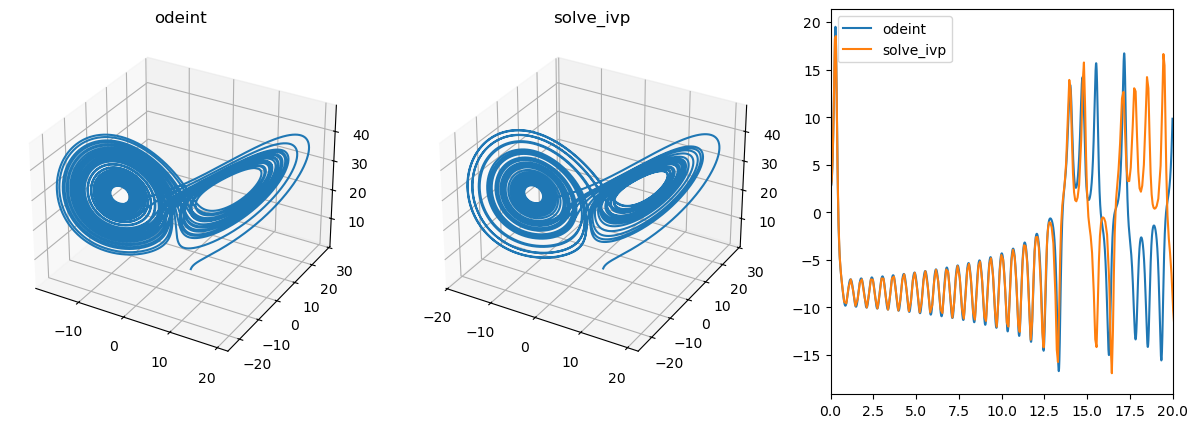
Решение на заданной временной сетке на примере аттрактора Лоренца

import numpy as np
from scipy.integrate import odeint, solve_ivp
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# Система: аттрактор Лоренца
def lorenz(t, state, sigma, beta, rho):
    x, y, z = state
    dx = sigma * (y - x)
    dy = x * (rho - z) - y
    dz = x * y - beta * z
    return [dx, dy, dz]

# Коэффициенты
sigma = 10.0
beta = 8.0 / 3.0
rho = 28.0

# Начальные условия
y0 = [3.0, 1.0, 1.0]

# Диапазон по времени
t_span = (0.0, 40.0)

# Сетка по времени
t = np.arange(t_span[0], t_span[1], 0.001)

# Решение на заданной сетке по времени
result_odeint = odeint(lorenz, y0, t, (sigma, beta, rho), tfirst=True)

fig = plt.figure(figsize=(15,5))
ax1 = fig.add_subplot(1, 3, 1, projection='3d')
ax1.plot(result_odeint[:, 0], result_odeint[:, 1], result_odeint[:, 2])
ax1.set_title("odeint")

# Решение на адаптивной сетке
result_solve_ivp = solve_ivp(lorenz, t_span, y0, args=(sigma, beta, rho), dense_output=True)
m = result_solve_ivp.sol(t)
ax2 = fig.add_subplot(1, 3, 2, projection='3d')
ax2.plot(m[0, :], m[1, :], m[2, :])
ax2.set_title("solve_ivp")

ax3 = fig.add_subplot(1, 3, 3)
ax3.plot(t, result_odeint[:, 0], label='odeint')
ax3.plot(result_solve_ivp.t, result_solve_ivp.y[0], label='solve_ivp')
ax3.set_xlim(0,20);
ax3.legend();

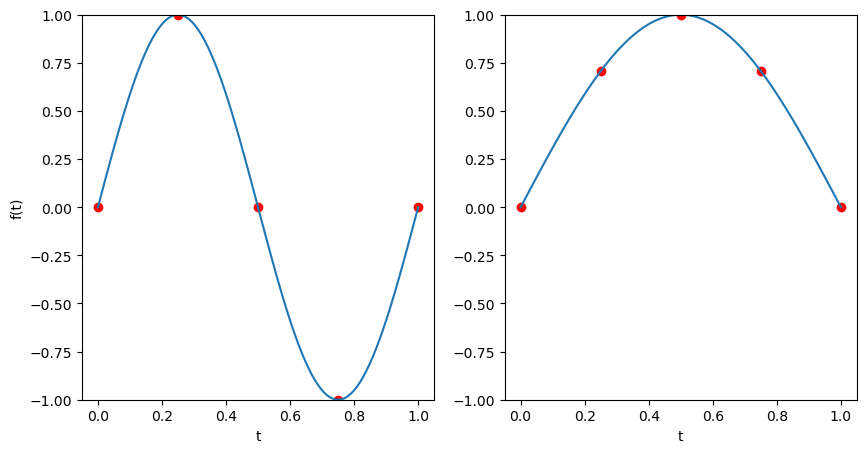
Решение с граничными условиями на примере задачи Штурма — Лиувилля

from scipy.integrate import solve_bvp
import matplotlib.pyplot as plt
import numpy as np

# Уравнение:
# y'' + k**2 * y = 0
def f(t, u, p):
    k = p[0]
    y0, y1 = u
    return np.vstack((y1, -k**2 * y0))

# Граничные условия:
# y(0) = y(1) = 0
# y'(0) = k
def bc(xa, xb, p):
    k = p[0]
    return np.array([xa[0], xb[0], xa[1] - k])

# Начальное предположение о f
t = np.linspace(0, 1, 5)
u = np.zeros((2, t.size))

x_plot = np.linspace(0, 1, 100)

fig = plt.figure(figsize=(10,5))

# Одно решение
u[0, 1] = 1
u[0, 3] = -1

sol = solve_bvp(f, bc, t, u, p=[6])

ax1 = fig.add_subplot(1, 2, 1)
ax1.plot(x_plot, sol.sol(x_plot)[0])
ax1.scatter(t, u[0], color='red')
ax1.set_xlabel("t")
ax1.set_ylabel("f(t)");
ax1.set_ylim(-1,1)

# Другое решение
u[0, 1] = np.sqrt(2)/2
u[0, 2] = 1
u[0, 3] = np.sqrt(2)/2

sol = solve_bvp(f, bc, t, u, p=[6])

ax2 = fig.add_subplot(1, 2, 2)
ax2.plot(x_plot, sol.sol(x_plot)[0])
ax2.scatter(t, u[0], color='red')
ax2.set_xlabel("t")
ax2.set_ylim(-1,1);

Численное решение дифференциальных уравнений в частных производных

Решение с использованием модуля findiff

from findiff import PDE, BoundaryConditions, FinDiff
from matplotlib import cm

shape = (100, 100)
x, dx = np.linspace(start=0, stop=1, num=shape[0], retstep=True)
y, dy = np.linspace(start=0, stop=1, num=shape[1], retstep=True)
X, Y = np.meshgrid(x, y, indexing="ij")

L = FinDiff(0, dx, 2) + FinDiff(1, dy, 2)
f = np.zeros(shape)

bc = BoundaryConditions(shape)
# Граничные условия Ньюмана
bc[1, :] = FinDiff(0, dx, 1), 0
bc[1:-1, -1] = FinDiff(1, dy, 1), 0
# Граничные условия Дирихле
bc[-1, :] = 300.0 - 200 * Y
bc[:, 0] = 300.0


pde = PDE(L, f, bc)
u = pde.solve()

plt.pcolor(X, Y, u);

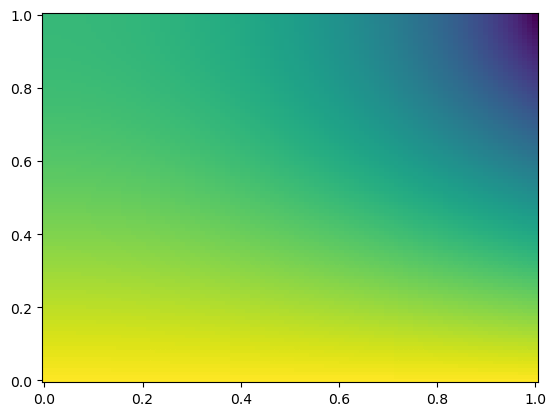
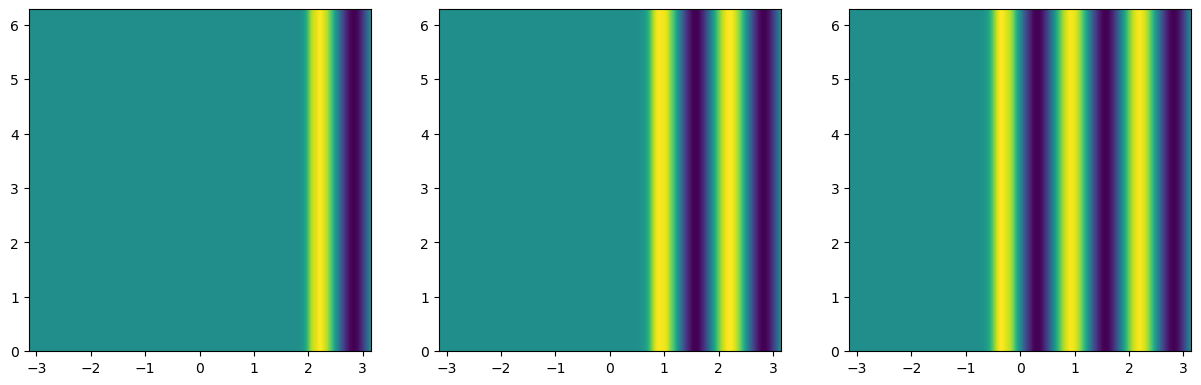
Решение с использованием модуля pde

import numpy as np
from pde import CartesianGrid, ScalarField, WavePDE, FieldCollection

x_range = [-np.pi, np.pi]
y_range = [0, 2*np.pi]

grid = CartesianGrid([x_range, y_range], [200, 200])
u = ScalarField(grid)
v = ScalarField(grid)
state = FieldCollection([u, v])

fig = plt.figure(figsize=(15,5))

eq = WavePDE(0.1, bc={"x": {"derivative": 0},"y-": {"value": 0}, "y+": {"value_expression": "sin(0.5*t)"}})
result = eq.solve(state, t_range=4*np.pi, dt=0.0005)
ax1 = fig.add_subplot(1, 3, 1)
ax1.imshow(result[0].data, extent= x_range+y_range, origin='lower')

result = eq.solve(result, t_range=4*np.pi, dt=0.0005)
ax2 = fig.add_subplot(1, 3, 2)
ax2.imshow(result[0].data, extent= x_range+y_range, origin='lower')

result = eq.solve(result, t_range=4*np.pi, dt=0.0005)
ax3 = fig.add_subplot(1, 3, 3)
ax3.imshow(result[0].data, extent= x_range+y_range, origin='lower');