Вычисления. Часть 1

Числовые данные

Встроенные средства Python не слишком хороши для работы с числовыми данными, поэтому для этого существуют отдельные модули. Наиболее важной из них является модуль NumPy, высокоэффективные методы для работы с числовыми массивам.

Массивы NumPy

Ключевой компонент NumPy — высокопроизводительные многомерные статические числовые массивы np.ndarray. Также в NumPy имеются многочисленные методы которые позволяют избежать накладных расходов при преобразовании np.ndarray к типам Python и обратно.

Некоторые свойства np.ndarray:

Свойство	Значение
a.ndim	Число измерений массива a
a.shape	Размер по осям (кортеж) массива a
a.size	Общее число элементов в a
a.dtype	Тип данных массива a

Создание массивов

import numpy as np

# Из списка Python
a = np.array([1,2,3,4,5])
print(a)

[1 2 3 4 5]

# Заполнение нулями
a = np.zeros(5)
print(a)

[0. 0. 0. 0. 0.]

# 5 точек от 0 до 5 включительно
a = np.linspace(0,5,5)
print(a)

[0.   1.25 2.5  3.75 5.  ]

# точки от 0 до 5 с шагом 1
a = np.arange(0,5,1)
print(a)

[0 1 2 3 4]

Многомерные массивы

Класс np.ndarray также позволяет работать с многомерными массивами. При этом задается параметр shape определяющий размерность.

import numpy as np

# Массив 2x3
a = np.zeros((2,3))
print(a)

[[0. 0. 0.]
 [0. 0. 0.]]

a = np.linspace(0,5,6)

# Изменение формы массива
b = a.reshape((3,2))
print(b)

[[0. 1.]
 [2. 3.]
 [4. 5.]]

# Изменение порядка осей
c = np.moveaxis(b,0,-1)
print(c)

[[0. 2. 4.]
 [1. 3. 5.]]

Индексация в массиве

При индексации сохраняется порядок индексов аналогичный фигуре

import numpy as np

b = np.linspace(0,5,6).reshape((3,2))
print(b)

[[0. 1.]
 [2. 3.]
 [4. 5.]]

# Один элемент
print(b[1,1])

3.0

# Все элементы по 1 оси, 1 элемент по 0 оси
print(b[1,:])

[2. 3.]

# Все элементы по 0 оси, 1 элемент по 1 оси
print(b[:,1])

[1. 3. 5.]

# Выборка и использованием срезов
v = b[1:-1,1]
print(v)

[3.]

В целях оптимизации срезы создают не копии np.ndarray, а так называемые представления (view), поэтому меняя данные в срезе они будут меняться и в исходном массиве.

Операции с массивами

В отличии от обычных списков Python операции над массивами производятся поэлементно.

import numpy as np

b = np.linspace(0,5,6).reshape((3,2))
print(b)

[[0. 1.]
 [2. 3.]
 [4. 5.]]

# Операция с числом
c = b + 2
print(c)

[[2. 3.]
 [4. 5.]
 [6. 7.]]

# Операция с массивом того-же размера
c = b * b
print(c)

[[ 0.  1.]
 [ 4.  9.]
 [16. 25.]]

В отличии от обычных списков Python операции над массивами производятся поэлементно.

Математические функции из math работать с np.ndarray не умеют, но в модуле numpy есть их аналоги (np.cos, np.log10, …).

Конкатенация

b = np.linspace(0,5,6).reshape((3,2))
print(b)

[[0. 1.]
 [2. 3.]
 [4. 5.]]

# Конкатенация по строкам
d = np.vstack((b,b))
print(d)

[[0. 1.]
 [2. 3.]
 [4. 5.]
 [0. 1.]
 [2. 3.]
 [4. 5.]]

# Конкатенация по столбцам
d = np.hstack((b,b))
print(d)

[[0. 1. 0. 1.]
 [2. 3. 2. 3.]
 [4. 5. 4. 5.]]

Итерация

NumPy предлагает альтернативный подход к итерации по всем элементам многомерного массива по сравнению с обычными вложенными циклами.

# Обычный обход. Получаем строки.
# Нужен вложенный цикл для доступа к элементам. Только чтение.
for x in b:
    print(x, end=" ")

[0. 1.] [2. 3.] [4. 5.] 

# Обход через np.nditer
for x in np.nditer(b):
     print(x, end=" ")

0.0 1.0 2.0 3.0 4.0 5.0 

# Обход через np.nditer с возможностью записи
for x in np.nditer(b, op_flags=['readwrite']):
    x[...] = 2 * x + 2
print(b)

[[ 2.  4.]
 [ 6.  8.]
 [10. 12.]]

# Многомерный аналог enumerate
for index, x in np.ndenumerate(b):
    print(index, x, end="; ")

(0, 0) 2.0; (0, 1) 4.0; (1, 0) 6.0; (1, 1) 8.0; (2, 0) 10.0; (2, 1) 12.0; 

Операции сравнения

Применение операций сравнения (>, <, >=, <=, ==, !=) к массивам np.ndarray вызывает создание массива значений типа bool соответствующего размера.

b = np.linspace(0,5,6).reshape((3,2))
t = b>3
print(t)

[[False False]
 [False False]
 [ True  True]]

Этот массив можно использовать далее для различных операций в качестве индекса.

q = b[b>3]
print(q)

[4. 5.]

b[b>3] = 0
print(b)

[[0. 1.]
 [2. 3.]
 [0. 0.]]

Маску можно использовать для любых массивов имеющих одинаковый shape. Их можно объединить в логические выражение с использованием операторов побитового «и» & и «или» |, а также использовать кванторы np.any и np.all.

Чтение и запись

Пример	Назначение
np.save('file.npy', m)	Сохранение данных из переменный m в файл формата Numpy
m = np.load('file.npy')	Чтение данных из формата Numpy в переменную m
np.savetxt('file.txt', m)	Сохранение данных из переменный m в текстовый файл
m = np.loadtxt('file.txt')	Чтение данных из текстового файла в переменную m
m.tofile('file.dat')	Сохранение данных в двоичный файл
m = np.fromfile('file.dat')	Сохранение данных в двоичный файл

Основные операции линейной алгебры в numpyЧто еще нужно знать о NumPy

• По NumPy есть подробная официальная документация

• Для работы с данными содержащими инвалидные значения существует специальный класс np.ma.masked_array

• Два числа с плавающий запятой могут быть равны только чудом, поэтому следует использовать np.isclose и явно указывать точность.

• Классы np.ndarray переопределяют вывод на печать. Поэтому сделав print вы увидите только часть элементов.

Основные операции линейной алгебры в NumPy

Операции над векторами

Положим что одномерные массивы a и b являются векторами в трехмерном пространстве:

import numpy as np

a = np.array([1,1,1])
b = np.array([2,-1,3])

Операция	Запись	Результат
Длина вектора	np.linalg.norm(a)	1.7320508075688772
Произведение вектора на скаляр	2*a	array([2, 2, 2])
Сумма векторов	a + b	array([3, 0, 4])
Скалярное произведение	np.dot(a,b)	4
Векторное произведение	np.cross(a,b)	array([ 4, -1, -3])

Операции над матрицами

Положим, что a — вектор, а m — матрица 3x3.

import numpy as np

a = np.array([1,1,1])
m = np.array([[1,0,1],[2,1,-1],[-1,0,-3]])

Операция	Запись	Результат
Определитель	np.linalg.det(m)	-2.0
След	np.trace(m)	-1
Форма	m.shape	(3, 3)
Векторно-матричное умножение	np.matmul(a, m)	array([ 2, 1, -3])
Матричное умножение	np.matmul(m,m)	array([[ 0, 0, -2], [ 5, 1, 4], [ 2, 0, 8]])
Обратная матрица	np.linalg.inv(m)	array([[ 1.5, 0. , 0.5], [-3.5, 1. , -1.5], [-0.5, 0. , -0.5]])
Собственные числа и собственные векторы	np.linalg.eig(m)	(array([ 1. , 0.73205081, -2.73205081]), array([[ 0. , 0.11727205, -0.2405126 ], [ 1. , -0.99260257, 0.36940291], [ 0. , -0.03142295, 0.89760524]]))
Транспонирование	m.T	array([[ 1, 2, -1], [ 0, 1, 0], [ 1, -1, -3]])
Нулевая матрица	np.zeros((3,3))	array([[0., 0., 0.], [0., 0., 0.], [0., 0., 0.]])
Единичная матрица	np.eye(3)	array([[1., 0., 0.], [0., 1., 0.], [0., 0., 1.]])
Удаление измерений состоящих из одного элемента	np.squeeze(np.array([[[1,2,3]]]))	array([1., 2., 3.])

Вращение координат

Вращение координат удобно задавать в виде матрицы поворота с помощью модуля scipy.spatial.transform:

import numpy as np
from scipy.spatial.transform import Rotation

#Вращение на 90 градусов вокруг оси X
m_rot = Rotation.from_euler('x', [np.pi/2]).as_matrix()

a = np.array([1,1,1])

rot_a = np.squeeze(np.matmul(a, m_rot))

Способы задания вращения

Способ задания	Описание	Пример
Углы Эйлера	Последовательность вращений вокруг осей координат	Rotation.from_euler('xy', [np.pi/2, -np.pi/6])
Матрица поворота	Матрица направляющих косинусов	Rotation.from_matrix([[0,0,0],[0,0,0],[0,0,1]])
Вращение вокруг вектора	Вращение вокруг вектора единичной длинны на данный угол	v = np.array([1, 0, 1]); Rotation.from_rotvec(np.pi/2 * v/np.linalg.norm(v))
Кватернион	Запись вращения в форме кватерниона (x, y, z, w)	Rotation.from_quat([0. , 0. , 0.70710678, 0.70710678])

Библиотека scipy.spatial.transform также позволяет преобразовывать одно представление вращения в другое методами to_euler, to_matrix, to_rotvec, to_quat.

Функция на сетке

Важная особенность np.ndarray — возможность обходиться при вычислении значения функции без циклов.

import numpy as np

def f(x,y):
    return x**2+2*x+6*y

s = np.linspace(1,7,3)
p = np.linspace(5,9,3)

v = f (s,p) # Функция f была применена поэлементно 
print(v)

[ 33.  66. 117.]

S, P = np.meshgrid(s,p,indexing='ij')
v = f (S,P) # Функция f была применена для каждой пары из s и p
print(v)

[[ 33.  45.  57.]
 [ 54.  66.  78.]
 [ 93. 105. 117.]]

В случае простой подстановки f(s,p) будет массивы будут подставлены поэлементно. В случае подстановки с использованием meshgrid из массивов будет построена сетка, в узлах которой будут пары элементов и функция будет рассчитана для каждого элемента сетки.

Дифференциальные операторы на сетке

Для расчетов производных на сетке будем использовать модуль findiff

import numpy as np
from findiff import FinDiff

x = np.linspace(0, 10, 100)
dx = x[1] - x[0]
f = np.sin(x)

d_dx = FinDiff(0, dx, 1)
df_dx = d_dx(f)

Объект FinDiff реализует дифференциальный оператор, аргументы: 0 — по первой оси, dx — размер шага, 1 — первая производная.

df_dx — массив np.ndarray со значениями производной f в узлах сетки. Модуль findiff не изменяет размер массива т.к. на краях применяется схема дифференциирование вперед или назад соответственно, а по остальному объему массива используется центральная схема.

Дифференциальные операторы модуля findiff

Название	Значение	Запись	Вход	Выход
FinDiff	производиная	d/dx	скалярное поле	скалярное поле
Gradient	градиент	∇f	скалярное поле	векторное поле
Laplacian	оператор Лапласа	∇2 f	скалярное поле	векторное поле
Divergence	дивергенция	∇· f	векторное поле	скалярное поле
Curl	ротор	∇×f	векторное поле	векторное поле

В 2D задаче

import numpy as np
from findiff import Gradient, Divergence, Laplacian
import matplotlib.pyplot as plt

borders = [-2*np.pi, 2*np.pi, -2*np.pi, 2*np.pi]

x = np.linspace(-2*np.pi, 2*np.pi, 30)
dx = x[1]-x[0]
y = np.linspace(-2*np.pi, 2*np.pi, 30)
dy = y[1]-y[0]

X, Y = np.meshgrid(x, y, indexing='ij')
f = Y*np.sin(X) + np.cos(Y)

plt.imshow(f.T,  origin='lower', extent=borders)
contours = plt.contour(X, Y, f,  origin='lower', colors = 'r')
plt.clabel(contours, colors = 'r')
plt.show()

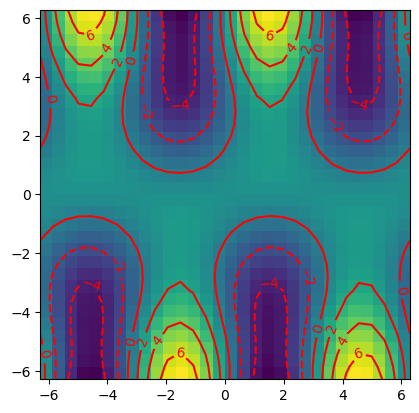
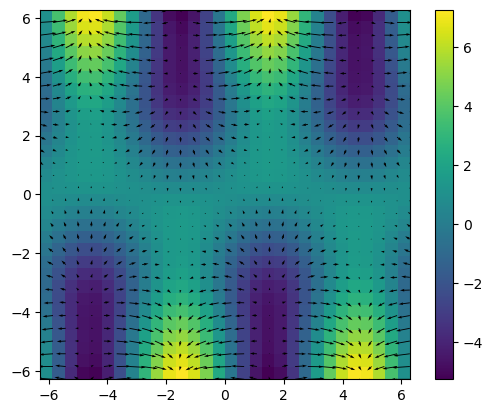
grad = Gradient(h=[dx, dy])
grad_f = grad(f)

plt.imshow(f.T ,  origin='lower', extent=borders)
plt.colorbar()
plt.quiver(X,Y,grad_f[0],grad_f[1])
plt.show()

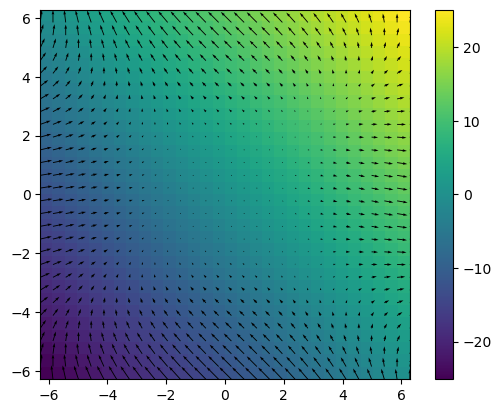
u = np.array((X**2-Y**2, Y**2-X))

div = Divergence(h=[dx, dy])
div_u = div(u)

plt.imshow(div_u.T,origin='lower', extent=borders)
plt.colorbar()
plt.quiver(X,Y,u[0],u[1])
plt.show()

В 3D задаче

import numpy as np
from findiff import Gradient, Divergence, Laplacian, Curl

x = np.linspace(0, 10, 100)
dx = x[1]-x[0]
y = np.linspace(0, 10, 100)
dy = y[1]-y[0]
z = np.linspace(0, 10, 100)
dz = z[1]-z[0]

X, Y, Z = np.meshgrid(x, y, z, indexing='ij')
f = np.sin(X) * np.cos(Y) * np.sin(Z)

grad = Gradient(h=[dx, dy, dz])
grad_f = grad(f)

laplace = Laplacian(h=[dx, dy, dz])
laplace_f = laplace(f)

g = np.array([f, 2*f, 3*f])

div = Divergence(h=[dx, dy, dz])
div_g = div(g)

curl = Curl(h=[dx, dy, dz])
curl_g = curl(g)