Вычисления. Часть 2#
Для решение многих вычислительных задач существует модуль scipy.
Численное решение уравнений#
В случае одной переменной#
import scipy.optimize
def foo(x):
y = 4*x+6
return y
# Найдем решение foo(x) = 0
# с начальным приближением x = 0
optobj = scipy.optimize.root(foo, 0)
if optobj.success:
print("x = ", optobj.x)
x = [-1.5]
Совместное решение системы уравнений#
import scipy.optimize
def func(d):
x,y = d
f1 = 2*x + 3*y
f2 = -x**2 + 3
return (f1,f2)
# Найдем решение foo(x,y) = 0
# с начальным приближением x = 5, y = 5
optobj = scipy.optimize.root(func, (5,5))
if optobj.success:
print("x = ", optobj.x)
x = [ 1.73205081 -1.15470054]
Минимизация функции#
import scipy.optimize
def f(c):
x, y = c
return 0.5*(1 - x)**2 + (y - x**2)**2
# Выполним минимизацию f(x,y) -> min
# с начальным приближением x = 2, y = -1
optobj = scipy.optimize.minimize(f, [2, -1])
if optobj.success:
print("x = ", optobj.x)
x = [0.99999991 0.99999979]
Решение системы линейных уравнений#
import numpy as np
import scipy.linalg
# Решаем систему Ax=B
# Переопределенная система
m = [[ 1, 3, 4],
[ 2, -3, 1],
[ -3, -4, 8],
[1.1, 2.9, 4.1]]
A = np.array(m)
B = np.array([ 0. , 1. , 2. , 0.1])
# Решение методом наименьших квадратов
x, res, rnk, s = scipy.linalg.lstsq(A,B)
print(x)
[ 0.07299771 -0.23112712 0.16181287]
Функция возвращает кортеж, важнейшие поля: значение, сумма ошибок и эффективный ранг матрицы.
Поиск оптимальных параметров#
import scipy.optimize
def foo(x, a, b, c):
return a*x**2+b*x+c
xdata = [0,2,4,6]
ydata = [6.1,9.9,29,65]
popt, pcov = scipy.optimize.curve_fit(foo, xdata, ydata)
print(popt)
[ 2.0125 -2.28500001 6.18000001]
Аргумент bounds метода curve_fit принимает кортеж из двух списков - минимальные и максимальные ограничения для значений каждой из переменных.
Фильтрация сигнала#
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
# Исходный сигнал
t = np.linspace(0,8*np.pi,800)
data = t+4*np.sin(t)*np.random.random(800)
#Фильтр Баттерворта
fs = 5 # Частота сигнала герцах
fc = 0.05 # Частота отсечения
# Частота в единицах отсчетов
# (одна для НЧ и ВЧ или кортеж из двух для полосового и режекторного фильтра)
w = fc / (fs / 2)
# Синтез НЧ фильтра 5-го порядка
b, a = signal.butter(3, w, 'low')
filtered = signal.filtfilt(b, a, data)
plt.plot(data)
plt.plot(filtered)
[<matplotlib.lines.Line2D at 0x7f793a3c20d0>]
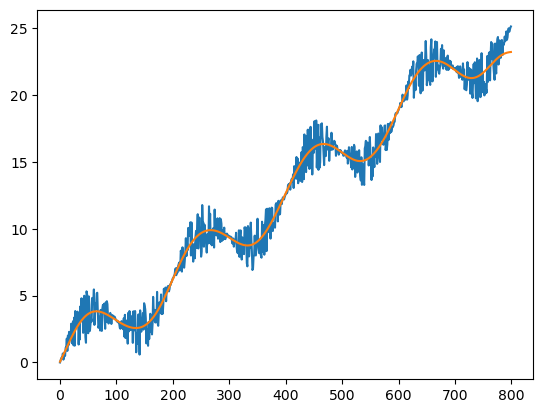
Сглаживание апериодического сигнала#
import numpy as np
import matplotlib.pyplot as plt
a = np.r_[np.arange(0,30,1),np.zeros((40,))+30,np.arange(30,60,1)]
plt.plot(a)
noise_a = a + np.random.random_sample(100)*16-8
plt.plot(noise_a)
def smooth(data, window_len = 10, tails = "odd"):
lead_0 = data[0]
lead = data[window_len//2-1:0:-1]
tail_0 = data[-1]
tail = data[-2:-window_len//2-2:-1]
if tails == "odd":
ds = np.r_[2*lead_0-lead, data , 2*tail_0-tail]
else:
ds = np.r_[lead, data , tail]
w = np.hanning(window_len)
return np.convolve(w/w.sum(), ds, mode='valid')
plt.plot(smooth(noise_a, 40, tails = "odd"))
[<matplotlib.lines.Line2D at 0x7f793a1e3750>]
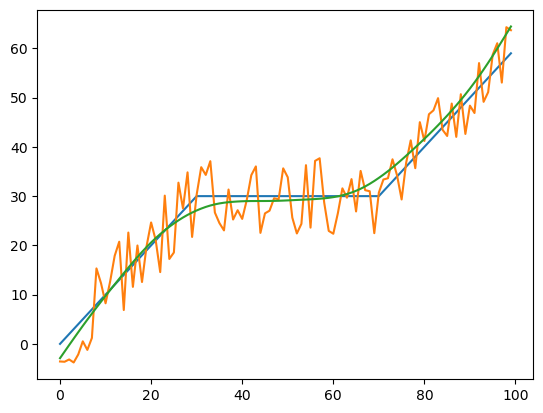
Анализ спектра сигнала#
Будем разлагать значения сигнала на сетке в спектр с помощью быстрого преобразования Фурье.
from scipy.fftpack import fft
x = np.linspace(0.0, 2, 600)
y = np.sin(15.0 * 2.0*np.pi*x) + np.sin(20.0 * 2.0*np.pi*x)
plt.plot(y)
[<matplotlib.lines.Line2D at 0x7f793a276990>]
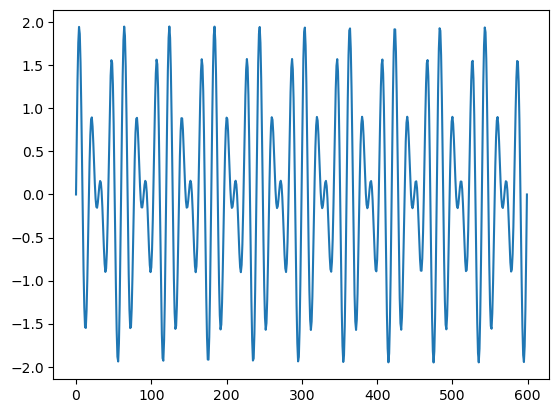
yf = fft(y)
plt.plot(np.abs(yf)[0:50])
[<matplotlib.lines.Line2D at 0x7f793a0ea990>]
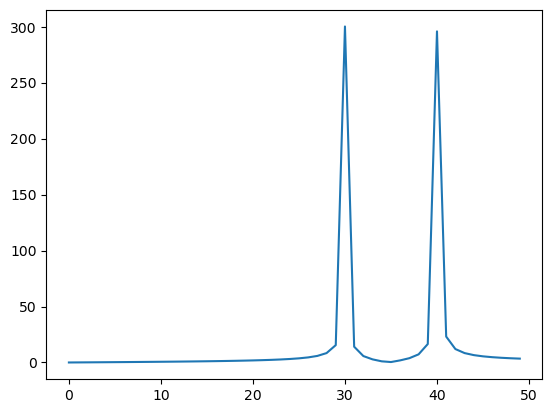
Расчет передаточной фукнции#
import control as ct
import matplotlib.pyplot as plt
num= [1., 2.]
den= [3., 4., 5.]
w= ct.tf(num, den)
print(w)
<TransferFunction>: sys[0]
Inputs (1): ['u[0]']
Outputs (1): ['y[0]']
s + 2
---------------
3 s^2 + 4 s + 5
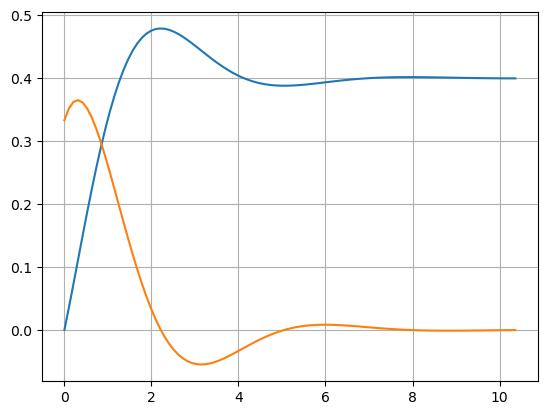
Реакция на изменение уровня и импульс входного сигнала#
x,y=ct.step_response(w)
plt.plot(x,y)
x,y=ct.impulse_response(w)
plt.plot(x,y)
plt.grid(True)
plt.show()
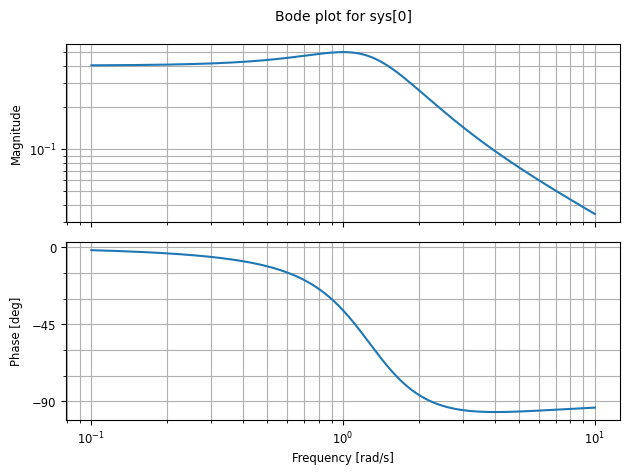
Амплитудно-частотная характеристика#
omega = np.logspace(-2, 2, 500)
response = ct.frequency_response(w, omega)
ct.bode_plot(w, initial_phase=0)
plt.show()
Интерполяция#
Будем рассматривать случаи получения функции в неявном виде.
В случае одной переменной#
import scipy.interpolate
x = np.arange(0, 10)
y = 2*x**3-16*x**2
foo = scipy.interpolate.interp1d(x, y)
print(foo(0.2))
-2.8000000000000003
В случае нескольких переменных на регулярной сетке#
from scipy.interpolate import RegularGridInterpolator, LinearNDInterpolator
import numpy as np
import matplotlib.pyplot as plt
def func(x, y):
return 8*x**2-y**3
xi = np.arange(-5,5,0.2)
yi = np.arange(-2,2,0.1)
grid_x, grid_y = np.meshgrid(xi, yi, indexing='ij')
#Прямой расчет на сетке
data = func(grid_x, grid_y)
# Интерполяция
foo = RegularGridInterpolator((xi,yi),data)
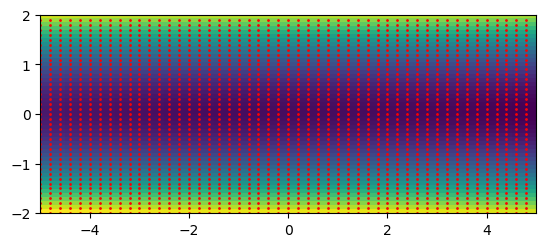
# исходное поле
plt.imshow(func(grid_x, grid_y), extent=[-5,5,-2,2], origin='lower')
# точки
plt.scatter(grid_x, grid_y, s=1, c ='red')
<matplotlib.collections.PathCollection at 0x7f7938859fd0>
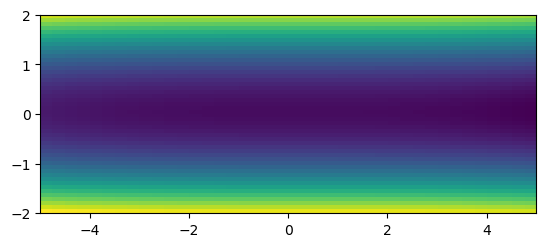
# результат интерполяции
plt.imshow(foo((grid_x, grid_y)), extent=[-5,5,-2,2], origin='lower')
<matplotlib.image.AxesImage at 0x7f7933b1ca50>
В случае нескольких переменных на случайных точках#
#Нерегулярная сетка
xs = np.random.uniform(-5, 5, 50)
ys = np.random.uniform(-2, 2, 50)
#Значение в точках
values = func(xs, ys)
# исходное поле
plt.imshow(func(grid_x, grid_y), extent=[-5,5,-2,2], origin='lower')
# точки
plt.scatter(xs, ys, s=1, c ='red')
# Линейная интерполяция на нерегулярной сетке
baz = scipy.interpolate.LinearNDInterpolator(np.rollaxis(np.array([xs,ys]), 1), values)
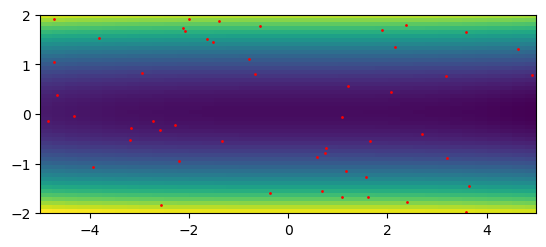
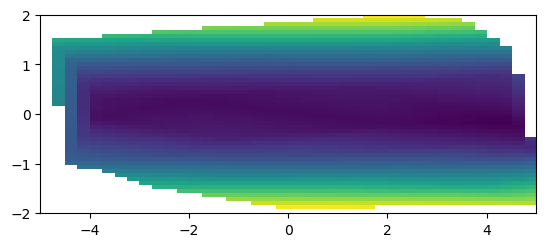
# результат интерполяции
plt.imshow(baz((grid_x, grid_y)), extent=[-5,5,-2,2], origin='lower')
<matplotlib.image.AxesImage at 0x7f7933bdcb90>
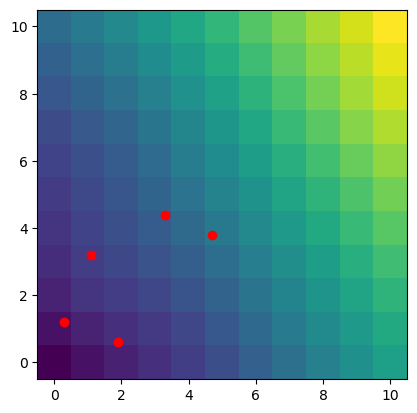
Кригинг#
Отличие от других методов интерполяции — наилучшее линейное несмещенное предсказание промежуточных значений. В scipy криггинга нет, но он есть в пакете pykrige.
import numpy as np
from pykrige.uk import UniversalKriging
# Значения в точках : x, y, value
data = np.array([[0.3, 1.2, 0.47],
[1.9, 0.6, 0.56],
[1.1, 3.2, 0.74],
[3.3, 4.4, 1.47],
[4.7, 3.8, 1.74]])
xi = np.arange(0.0, 5.5, 0.5)
yi = np.arange(0.0, 5.5, 0.5)
# Подготовка объекта кригинга
UK = UniversalKriging(data[:, 0], data[:, 1], data[:, 2],
variogram_model='linear',
drift_terms=['regional_linear'])
# Кригинг
z, ss = UK.execute('grid', xi, yi)
grid_x, grid_y = np.meshgrid(xi, yi, indexing='ij')
plt.scatter(data[:, 0], data[:, 1], c = 'red')
plt.imshow(z, origin='lower')
<matplotlib.image.AxesImage at 0x7f7933a51590>
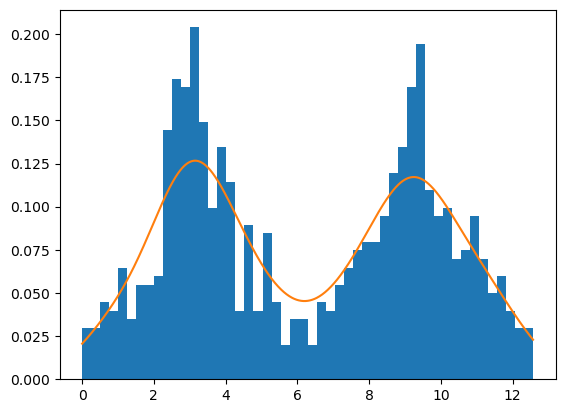
Построение функции плотности распределения#
from scipy import stats
# data - массив измерений
# В данном примере одномерный, но многомерные тоже поддерживаются
t = np.linspace(0,4*np.pi,800)
data = t+4*np.sin(t)*np.random.random(800)
kde = stats.gaussian_kde(data)
x_grid = np.linspace(min(data),max(data), 1000)
kde_vals = kde.evaluate(x_grid)
plt.hist(data, bins=50, density=True)
plt.plot(x_grid,kde_vals)
[<matplotlib.lines.Line2D at 0x7f7933b41d10>]
Символьные вычисления#
Помимо численных расчетов для Python существует достаточно простая система символьной математики sympy.
import sympy
from sympy import oo, Symbol
x = sympy.Symbol('x')
y = sympy.Symbol('y')
# Важно! eq не значение выражения справа,
# а специальный объект типа sympy.equation
eq = y**2+x
print(eq.subs(x,2).subs(y,3).evalf())
11.0000000000000
eq2 = 1/( (x + 2)*(x + 1) )
print(sympy.apart(eq2, x))
-1/(x + 2) + 1/(x + 1)
# Предел
sympy.limit(sympy.sin(x)/x, x, 0)
\[\displaystyle 1\]
# Производная
sympy.diff(sympy.tan(x), x)
\[\displaystyle \tan^{2}{\left(x \right)} + 1\]
# Сумма ряда
i = sympy.Symbol('i')
sympy.summation(1/2**i, (i, 0, oo))
\[\displaystyle 2\]
# Первообразная
sympy.integrate(2*x + sympy.sinh(x), x)
\[\displaystyle x^{2} + \cosh{\left(x \right)}\]